Normalmente encontramos as demonstrações para a lei dos cossenos a partir de um triângulo acutângulo qualquer, e para um dos lados apenas, mas, neste post, vou fazer a demonstração para o triângulo obtusângulo, para os três lados. O faço inspirada pelas excelentes discussões com a turma 2024 do PROFMAT, para a qual eu leciono a disciplina de Geometria.
A partir de um triângulo obtusângulo ABC, de lados a, b e c, a oposto a Â, b oposto a ^B e c oposto a ^C. Queremos provar (é a nossa Tese):
- a²=b²+c²-2bc.cosÂ
- b²=a²+c²-2ac.cos^B
- c²=b²+a²-2ba.cos^C
a²=b²+c²-2bc.cosÂ
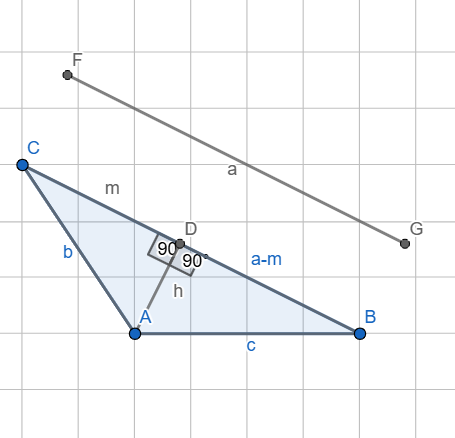
Para este caso eu pensei na seguinte configuração, uma vez que eu preciso de dois triângulos retângulos, pra usar Pitágoras e obter os a², b² e c² que eu preciso e do cos Â, coloquei a altura, em relação ao lado AB e chamei de m a extensão que fiz para o lado AB. Esta é a nossa hipótese, vamos partir dela.
Veja que, com isso, eu tenho um ângulo Â' que é suplementar do ângulo Â, cujo cosseno nos interessa. cos Â'=m/b e, isolando m, m=b.cos Â', e mais importante, m=-b.cos (I) [porque o que nos interessa é o cosseno do suplementar de Â', é ele o nosso ângulo de interesse], reserve.
Agora, vamos ao círculo trigonométrico para ver que cosÂ=-cosÂ'. Veja que temos o mesmo ângulo se deslocando no círculo trigonométrico, apenas o que muda é a orientação no eixo dos cossenos, que para um ângulo alfa qualquer é positiva e para 180º-alfa é negativa.
Retomando
Daqui já retiramos, por Pitágoras, b²=h²+m² (II), reserve.
Agora vamos ao triângulo DCB, que tem coisas que nos interessam: h, m, c e a.
a²=(m+c)²+h² (III), reserve.
Temos tudo o que precisamos agora:
m=-b.cos  (I)
b²=h²+m² (II)
a²=(m+c)²+h² (III)
Reta final agora, como estamos em busca de
- a²=b²+c²-2bc.cosÂ, que é a nossa tese.
Vamos começar por III , que já começa com a²=..., e vamos fazendo substituições.
a²=(m+c)²+h², desenvolvendo, a²=m²+2mc+c²+h² (precisamos arrumar um jeito de sumir com m², não tem m² na tese, e também precisamos ficar com -2bc no final, vamos encaminhar a nossa prova por aí).
De II, isolando h², temos: h²=b²-m², o que já é bom porque vai cancelar o m² que precisa sumir em III (justamente o que precisavamos).
a²=m²+2mc+c²+h², de II: h²=b²-m², substituindo II em III, temos:
a²=m²+2mc+c²+b²-m² (veja que aqui vamos conseguir cancelar m² e já temos a², b² e c², falta só o nosso -2bc.cosÂ, mas ele, lá do ângulo suplementar, virá). Vamos usar I em III.
a²=+2mc+c²+b², como m=-b.cos (I), chegamos à nossa tese.
a²=-2bc.cosÂ+b²+c², reorganizando, pra ficar bonitinho.
a²=b²+c²-2bc.cosÂ.
CQD.
b²=a²+c²-2ac.cos^B
Para o lado b eu pensei nos triângulos ADC e BEC para conseguir a², b², c² e cos^B. Trabalhei aqui com o fato de que o seno de um ângulo é o cosseno do seu complementar [THE JUMP OF THE CAT] (isso acontece porque em um triângulo retângulo os demais ângulos internos só podem somar 90º e por isso são complementares, como o cateto oposto de um ângulo é o cateto adjacente do outro, a mágica acontece, eu trato mais detalhadamente deste tema neste texto)
Vamos, por Pitágoras, calcular, considerando que CD=BE=h:
Para CDA, b²=m²+h² (I)
Para BEC, a²=(c+m)²+h² (II)
E, também, o seno de ^B'= (m+c)/a e o cos^B= (m+c)/a, isolando m, temos: m=a.cos^B-c (III)
Agora vamos começar já a montar o nosso quebra cabeças pra chegar na tese. Vamos começar por I, que já tem o b²=... que queremos.
b²=m²+h² e de II, temos, h²=a²-(c+m)².
Substituindo II em I.
b²=c²+a²-(c+m)²
Desenvolvendo.
b²=m²+a²-c²-2mc-m².
Simplificando, fazendo m²-m²
b²=+a²-c²-2mc.
Parece que ficou tudo meio fora de lugar, mas calma que tudo vai se ajeitar, vamos pegar III e colocar na nossa equação, que vai dar certo, veja que tem um 2c que vai multiplicar a.cos^B-c.
b²=a²-c²-2c(a.cos^B-c)
Desenvolvendo
b²=a²-c²-2ca.cos^B+2c²
Simplificando, fazendo -c²+2c², chegamos na nossa tese.
b²=a²+c²-2ac.cos^B.
CQD.
c²=b²+a²-2ba.cos^C
Nesta prova, o pulo do gato (como diz o professor Mathias: The jump of the cat) está em usar a altura h a partir do lado CB, e mais, é necessário que o segmento a-m esteja no triângulo ABD porque precisamos de a² positivo e se ele estiver no triângulo ACD teremos, no desenvolvimento da prova, ao final, -a², que não nos interessa. Inclusive é por isso que a altura deve ser em relação a CB e estar interna no triângulo ACB.
Como já dito anteriormente, a gente precisa de dois triângulos retângulos para a gente usar o Teorema de Pitágoras e obter os c², b², a² e poder achar fácil cos ^C. Então, vamos ao que precisamos.
Por pitágoras:
No triângulo ACD, temos: b²=m²+h² (I)
No triângulo ABD, temos: c²=(a-m)²+h² (II) [Veja que é importante que (a-m) esteja neste triângulo, senão teremos problemas na hora de conseguir o a² e na hora de eliminar o m²].
Vamos já aproveitar e registrar o CosC=m/b, de isolar m, ficando com m=bcosC (III).
Agora, usando II, porque já temos c²=... e, isolando h² em I, h²=b²-m² e substituindo em II, veja que m² já vai sumir, e, vamos chegando ao que queremos (nossa tese).
c²=(a-m)²+b²-m²
desenvolvendo (a-m)², temos:
c²=a¹-2am+m²+b²-m²
simplificando, temos:
c²=a¹-2am+b²
Usando III, que já, marotamente a gente já tinha isolado m, ficando com m=b.cos^C, nós chegamos à nossa tese.
c²=a¹+b²-2ab.cosC.
CQD.
Agradecimentos
À turma 2024 do PROFMAT CAMPUS SÃO GONÇALO, cuja diligência e dedicação tanto enriqueceram a disciplina. A demonstração para c foi proposta pelo mestrando Ricardo Barbosa Silva, e, também, a turma ofereceu outras tantas excelentes possibilidades para as demonstrações aqui apresentadas.
Nota 1:
Optamos por iniciar a demonstração com o caso de triângulos obtusângulos porque ele exige o uso completo da definição do cosseno no círculo trigonométrico, abrangendo situações onde cosÂ<0\cos A < 0. Esta abordagem demonstra a generalidade da Lei dos Cossenos, sendo válida também para os casos de triângulos acutângulos e retângulos como casos particulares.
Nota 2:
Sobre a generalidade da demonstração:
A Lei dos Cossenos é válida para qualquer triângulo (acutângulo, obtusângulo ou retângulo). Nesta demonstração, focamos no caso dos triângulos obtusângulos porque ele inclui a complexidade adicional de quando o cosseno de um ângulo interno é negativo (cos  < 0).
No caso dos triângulos acutângulos, onde cos  > 0, os mesmos princípios geométricos e trigonométricos apresentados aqui são aplicáveis sem alterações. Assim, a demonstração realizada para triângulos obtusângulos também é válida para triângulos acutângulos, dispensando uma prova separada.
A autora
Daniela Mendes Vieira da Silva é doutora pelo programa de pós graduação em ensino de Matemática da UFRJ, professora adjunta do departamento de Matemática da FFP/UERJ, coordenadora geral do projeto de extensão LEM FFP UERJ ITINERANTE e do projeto de pesquisa e iniciação científica, fomentado pela FAPERJ e pela UERJ, Matemática e Física na mala. É também líder do grupo de pesquisa em aprendizagem e ensino de Matemática da FFP-UERJ (GPAEM-FFP), coordenadora do Programa de Mestrado Profissional em Matemática em Rede Nacional (Profmat) na FFP/UERJ e diretora da Sociedade Brasileira de Educação Matemática (Regional Rio de Janeiro), eleita para o triênio 2025-2027.